First Intuitions of Homotopy Type Theory (HoTT)

What is a problem? A problem is a partial statement with high ambiguity. Solving a problem is akin to defining it rigorously. When we translate this reasoning into mathematics, we get the Curry–Howard Correspondence. This, I believe, is one of the most appealing aspects of Homotopy Type Theory(HoTT) and constructive mathematics in general. Consider the toy example of “Why does a ball roll down a hill?” If you started to expand your definitions, you’d answer the question — if we define what “roll down,” “ball,” and “hill,” the answer falls out at us. In a way we construct the solution to the problem by defining it. As another example, in software we experience this all the time. A client gives us a high level functional specification of a software system which we as programmers must turn into a rigorous definition via code. In fact, type theory and programming languages are intimately related. The other appealing thing about HoTT for me is that its fundamental objects, homotopy types, have a spacial interpretation which lends itself intuitively to many diverse problems.
When I first started reading the HoTT Book a lot of intuition alarm bells started going off, especially in respect to modern machine learning.
The topological interpretation of type theory that homotopy types gives us is strikingly relevant to neural networks. Neural networks are universal function approximators. Functions, given the co-domain and domain, define a particular type of space. When we train the parameters of a neural network by feeding it data, we slowly shape a space that gets closer and closer to the function that produced the input data. Some topological process is taking place in neural network learning. I believe with HoTT serving as a replacement for the foundations of mathematics which formulations of set theory like ZFS has served, which both have roots in avoiding Russell’s Paradox, we will gain a tool set for solving problems that is more in line with our intuitions and were previously muddled town by set theoretic formulations. Just like different branches of mathematics have evolved to study different mathematical objects which lend themselves to formulating and solving different problems. Sure you can encode a graph theory problem in set theory, but sometimes our intuition can just make larger strides when reasoning about vertices and edges. Alan Turning’s Turing Machines and Church’s Lambda Calculus offer us another example of different but equivalent foundations (via the Church-Turing Thesis ) that lend themselves to reasoning about a domain in different ways.
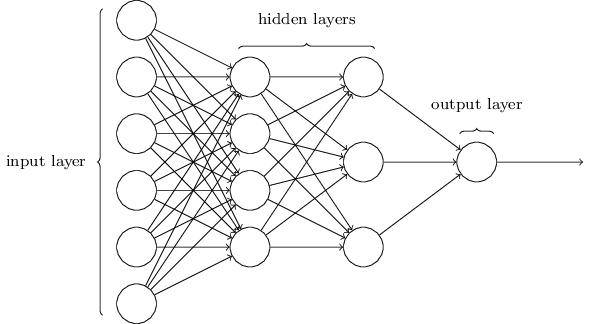
Neural networks have been vastly expanded since their original conception. Now we have all sorts of neural networks for doing different things. I’ve spent the last year studying different neural networks because they have been in most ground breaking research papers. One of the main issues everyone brings up at conferences or at meetups when neural networks are discussed is that they don’t have a rigorous mathematical theory supporting them, which leads to people feeling uneasy about trusting the learned results because the result of the learning process is a matrix of weights that cannot be reasoned with easily. We can only statistically check for overall error in tasks like classification. Among others, there is an ongoing effort by DARPA called eXplainable AI (XAI) which aims to produce a new breed of system that enables us to reason with the results of the learning process.
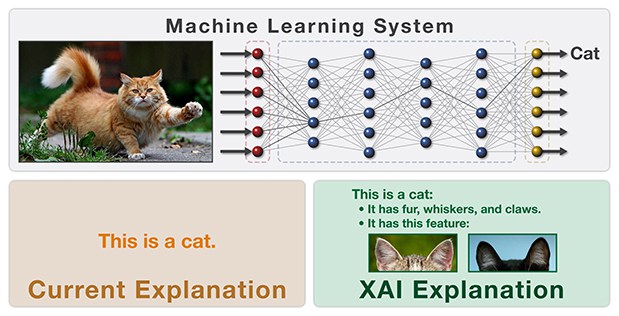
In sum, I’m excited for HoTT because I believe it will serve as a rigorous mathematical foundation for artificial intelligence in the coming years. The closest thing I have found to a formalization of deep learning has been energy-based models, and with contrastive divergence, they show dramatically the spacial nature of learning.
10/6/2017 Update: RIP Vladimir Voevodsky. He was a fundamental contributor to the ideas underlying HoTT.
